Ph. D. student LAN Haiqiang and his teacher ZHANG Zhongjie present a high-order fast-sweeping scheme to solve the Topography-dependent eikonal equation (TDEE) with the aim of achieving high-order accuracy in the travel-time calculation.
The scheme takes advantage of high-order weighted essentially nonoscillatory (WENO) derivative approximations, monotone numerical Hamiltonians, and Gauss Seidel iterations with alternating-direction sweepings. It incorporates high-order approximations of the derivatives into the numerical representation of the Hamiltonian such that the resulting numerical scheme is formally high-order accurate and inherits fast convergence from the alternating sweeping strategy. Extensive numerical examples are presented to verify its efficiency, convergence, and high-order accuracy.
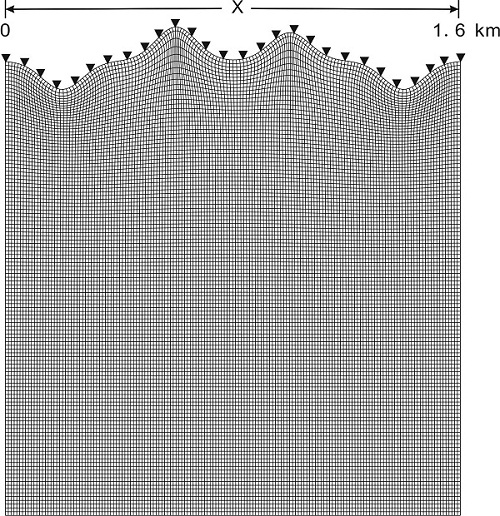
Figure 1. The mesh boundary-conforming grids for the models. (Image by LAN)
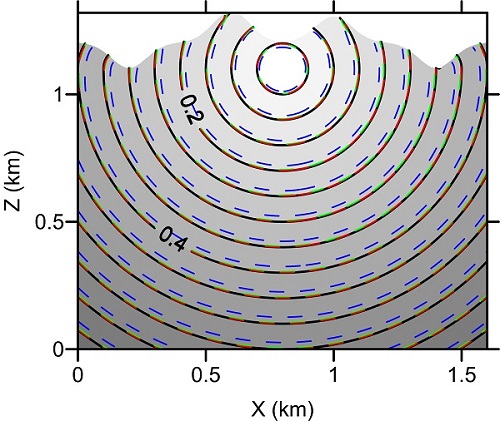
Figure 2. Travel-time contours (in seconds) for the group 3 model. (Image by LAN)
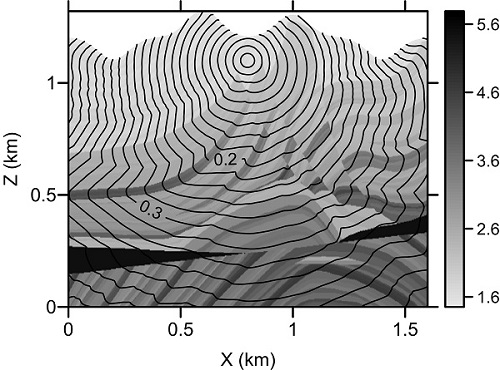
Figure 3. Travel-time contours (in seconds) for the Marmousi model. (Image by LAN)
Lan and Zhang.Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface. Geophysical Journal International, 2013, 193: 1010-1026 (Link)
Lan and Zhang. A High-Order Fast-Sweeping Scheme for Calculating First-Arrival Travel Times with an Irregular Surface. Bulletin of the Seismological Society of America, 2013, 103(3): 2070-2082 (Download Here)