Vice Professor ZHANG Jinhai and his teacher YAO Zhenxing optimize the constant coefficients of conventional finite-difference (FD) operator by maximizing the wavenumber coverage to reduce numerical dispersions in the presence of high-frequency components.

They set up three general criteria to enhance the convergence of the algorithm and reduce the optimization effort. They selected the error limitation to be 0.0001, this being the smallest in the literature, which led to perfect agreement between theoretical analyses and numerical experiments. The accuracy of their optimized FD methods can even reach that of much higher order unoptimized FD methods, which means great savings of computational efforts and memory demand. These advantages become even more apparent with 3D modeling, especially for saving memory demand.

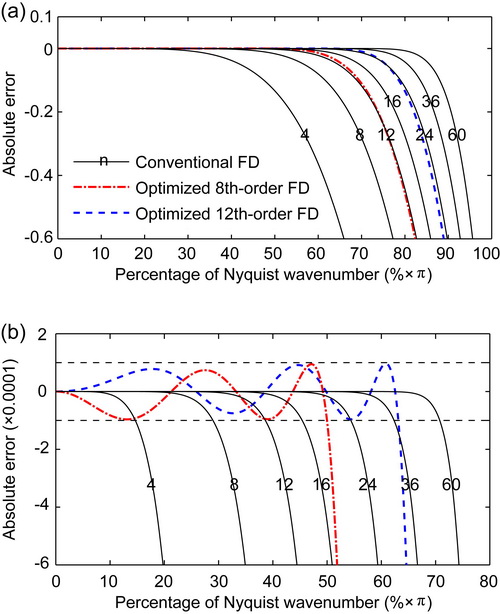
Figure 1. Accuracy comparison between the conventional and optimized FD operators. (Image by ZHANG)

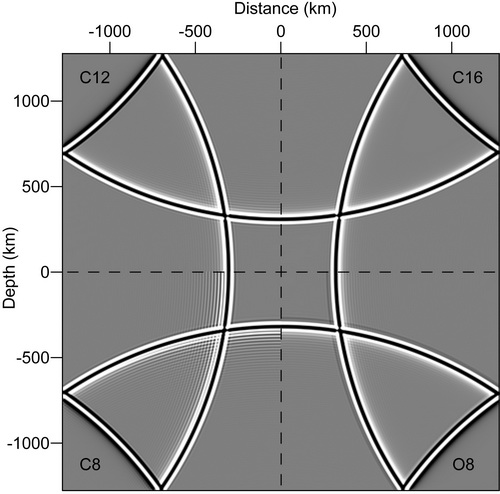
Figure 2. Impulse responses before and after using our optimization scheme. (Image by ZHANG)

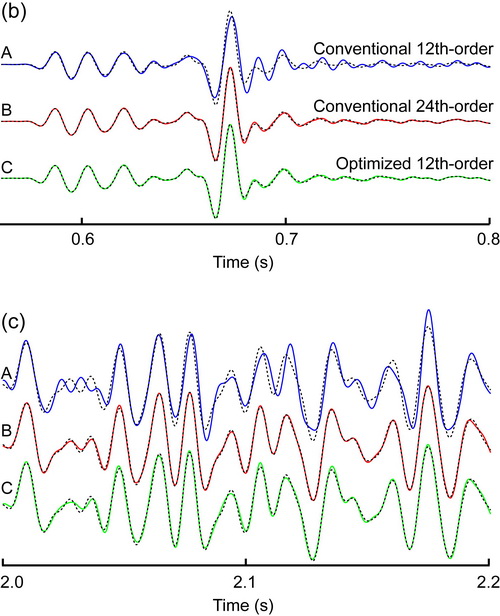
Figure 3. Waveform comparison among different methods within three time windows. (Image by ZHANG)

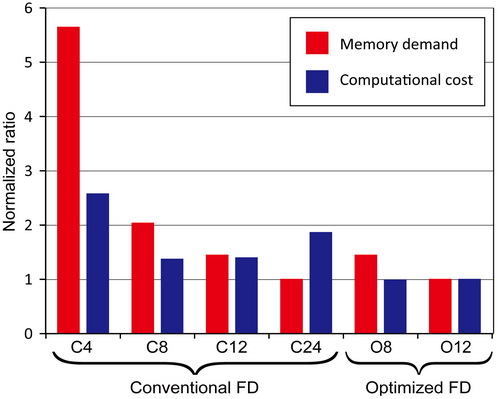
Figure 4. A comparison of memory demand and computational cost among different methods. (Image by ZHANG)

Zhang et al. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics. 2013, 78(1):13–18 （Download Here）