Professor LI Xiaofan and his team introduce the so-called symplectic discrete singular convolution differentiator (SDSCD) method for structure-preserving modelling of elastic waves.

Elastic wavefield modelling experiments on a laterally heterogeneous medium with high parameter contrasts demonstrate the superior performance of the SDSCD for suppression of numerical dispersion. Long-term computational experiments exhibit the remarkable capability of the approach presented for long-time simulations. Promising numerical results suggest the SDSCD is suitable for high-precision and long-time numerical simulations, as it has structure-preserving property and it can suppress effectively numerical dispersion when coarse grids are used.

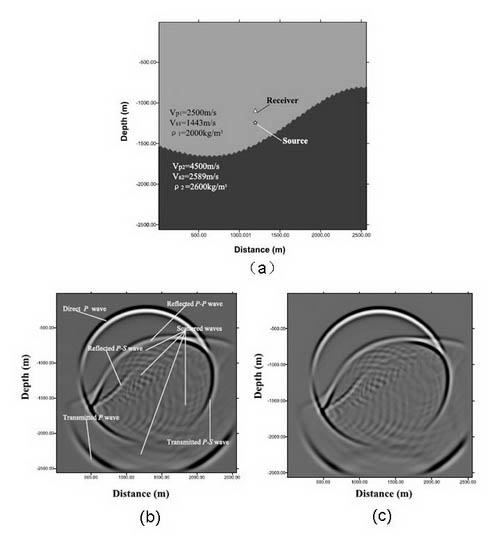
Figure 1. Snapshots of elastic wavefields (vertical component) in a lateral heterogeneous medium model at time 400 ms generated by SDSCD and the Fourier pseudospectral method. (Image by LI)

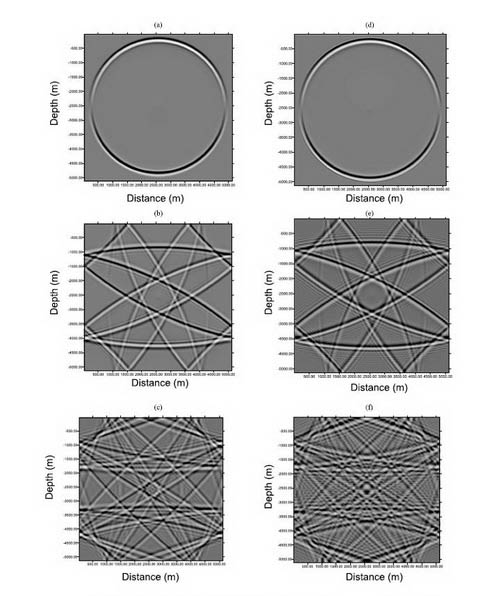
Figure 2. Snapshots of elastic wavefields (vertical component) in a 2-D homogeneous medium model generated by SDSCD and by the Fourier pseudospectral method after different time steps. (Image by LI)

Li et al. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophysical Journal International.2012, 188: 1382–1392 (Download Here)