Geophysical Prospecting, 2009, 57: 931-941

Lax-Wendroff and Nyström methods for seismic modelling

Chen, Jing-Bo

Abstract

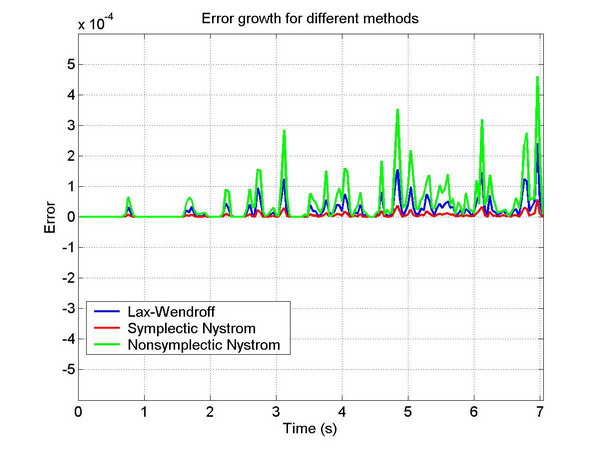
Lax-Wendroff and Nyström methods are numerical algorithms of temporal approximations for solving differential equations. These methods provide efficient algorithms for high-accuracy seismic modeling. In the context of spatial pseudospectral discretizations, I explore these two kinds of methods in a comparative way. Their stability and dispersion relation are discussed in detail. Comparison between the fourth-order Lax-Wendroff method and a fourth-order Nyström method shows that the Nyström method has smaller stability limit but has a better dispersion relation, which is closer to the sixth-order Lax-Wendroff method. The structure-preserving property of these methods is also revealed. The Lax-Wendroff methods are a second-order symplectic algorithm, which is independent of the order of the methods. This result is useful for understanding the error growth of Lax-Wendroff methods. Numerical experiments based on the scalar wave equation are performed to test the presented schemes and demonstrate the advantages of the symplectic methods over the nonsymplectic ones.